
The number of combinations of k objects from a set with n objects is n C k. The key here is without regard for order. It may help to think of combinations as a committee. Such selections are called combinations or k-sets. Therfore, The number of permutations of n distinct objects taken k at a time can be written as:Ĭombinations: There are many problems in which we are interested in determining the number of ways in which k objects can be selected from n distinct objects without regard to the order in which they are selected.
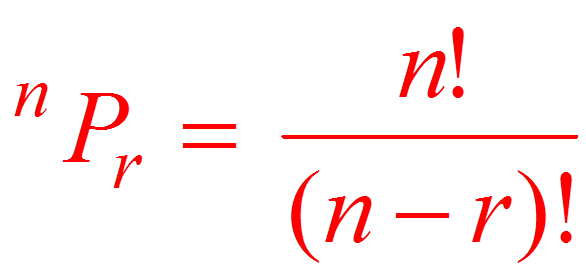
The number of ways of lining up k objects at a time from n distinct objects is denoted by n P k, and by the preceding we have: A combination is a selection of objects from a set of objects, that is objects are chosen from a particular set and listed, but the order in which the objects are listed is immaterial.
That is, the objects are chosen from a particular set and listed in a particular order. Permutations versus Combination: A permutation is an arrangement of objects from a set of objects. Notice that by convention, 0 ! = 1, (i.e., 0 ! º 1). The total number of ways that the parts can be selected is 4×3×5×4 or 240 ways.įactorial Notation: the notation n ! (read as, n factorial) means by definition the product: Numerical Example: A quality control inspector wishes to select one part for inspection from each of four different bins containing 4, 3, 5 and 4 parts respectively. This simple rule can be generalized as follow: If an operation consists of k steps, of which the first can be done in n1 ways and for each of these the second step can be done in n2 ways, for each of these the third step can be done in n3 ways and so forth, then the whole operation can be done in n1 × n2 × n3 × n4 ×. But often the numbers are just too large to count in the 1, 2, 3, 4 ordinary ways.Ī Fundamental Result: If an operation consists of two steps, of which the first can be done in n1ways and for each of these the second can be done in n2 ways, then the entire operation can be done in a total of n1× n2 ways. You may ask, why combinatorics? If a sample spaces contains a finite set of outcomes, determining the probability of an event often is a counting problem. Therefore, One of the basic problems of combinatorics is to determine the number of possible configurations of objects of a given type.
#10 PERMUTE 3 HOW TO#
Its objective is: How to count without counting. Many disciplines and sciences require the answer to the question: How Many? In finite probability theory we need to know how many outcomes there would be for a particular event, and we need to know the total number of outcomes in the sample space.Ĭombinatorics, also referred to as Combinatorial Mathematics, is the field of mathematics concerned with problems of selection, arrangement, and operation within a finite or discrete system. Thats why you should use empty directories.The following is a collection of JavaScript for computing permutations and combinations counting with or without repetitions. NOTE: splitlen does not append, it overwrites the files in the outdir. The best way to organize your dictionaries for use with oclHashcat is to sort each word in your dictionary by its length into specific files, into a specific directory, and then to run oclHashcat in directory mode.Īll you need to do is to create a new directory, for example “ldicts”. OclHashcat has a very specific way of loading dictionaries, unlike CPU hashcat. Note: this optimization is no longer needed by modern hashcat. This program is designed to be a dictionary optimizer for the now-deprecated oclHashcat.


 0 kommentar(er)
0 kommentar(er)
